이 문제는 이전에 해결한 적이 있지만 이전 해결 방법이 불친절(?) 했기 때문에 더 자세한 해결 방법을 남겨두겠습니다.
(문제)
https://school.programmers.co.kr/learn/courses/30/lessons/43105
코딩 테스트 연습 – 정수 삼각형
((7), (3, 8), (8, 1, 0), (2, 7, 4, 4), (4, 5, 2, 6, 5)) 30
school.programmers.co.kr
(이전 솔루션)
https://yummy0102.395
(DP) 정수 삼각형 – JAVA
https://school.programmers.co.kr/learn/courses/30/lessons/43105 프로그래머 모집 코드 지향 개발자입니다. 배치 기반 위치 매칭. 개발자 맞춤형 프로그래머 프로필에 가입하고,
yummy0102.tistory.com
다음은 문제 해결 방법을 고민하다가 정리한 노트입니다!
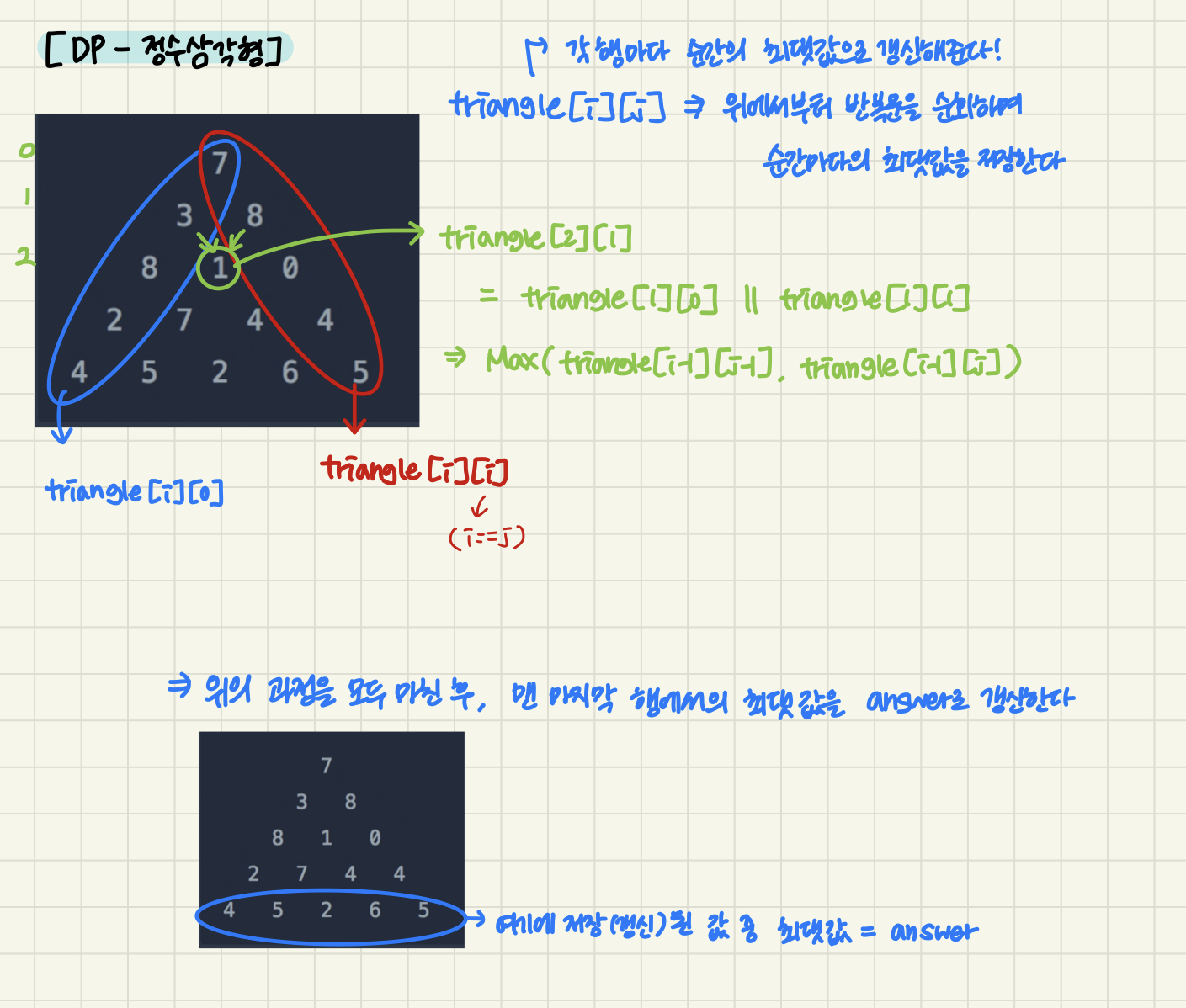
이제 위의 필기를 순서대로 풀고 다시 생각해보자!
DP용 메모이제이션 배열 정의
DP 문제의 특성상 이전 값을 저장할 배열을 정의해야 합니다.
이 문제의 경우 삼각형의 상단에서 하단까지 각 행에 숫자를 추가하여 얻을 수 있는 최대값을 찾아야 합니다.
그래서 우리는 주어진 2차원 배열 int()() 삼각형을 사용합니다!
삼각형(i)(j)는 위에서부터 해당 위치까지 삼각형의 수를 더할 때 최대값을 저장합니다!
사례수 공유
먼저 삼각형의 상단에서 아래로 내려가는 숫자를 선택하여 더할 수 있는 가능성의 수를 나눕니다.
스포일러, 총 3가지 경우가 있습니다!
1. 삼각형(i)(0)

첫 번째는 위와 같이 가장 왼쪽의 숫자를 더한 경우입니다.
위의 경우 더하는 유일한 방법은 바로 위에 있는 숫자를 더하는 것입니다.
따라서 열의 첫 번째 숫자인 경우 바로 위의 행과 동일한 열에 있는 숫자를 추가하면 됩니다.
재귀 수식의 형태로 표현:
// j==0 인 경우
triangle(i)(j) += triangle(i-1)(j)
2. 삼각형(i)(i)

두 번째 경우는 마지막 열 번호의 경우 첫 번째 경우와 유사합니다.
다시 말하지만 위에서 아래로 더할 수 있는 유일한 숫자는 바로 위에 있는 숫자입니다.
따라서 각 행의 마지막 열에 있는 숫자의 경우 바로 위에 있는 숫자를 더합니다.
재귀 수식의 형태로 표현:
// i==j 인 경우
triangle(i)(j) += triangle(i-1)(j-1)
3. 최대(삼각형(i-1)(j-1), 삼각형(i-1)(j))
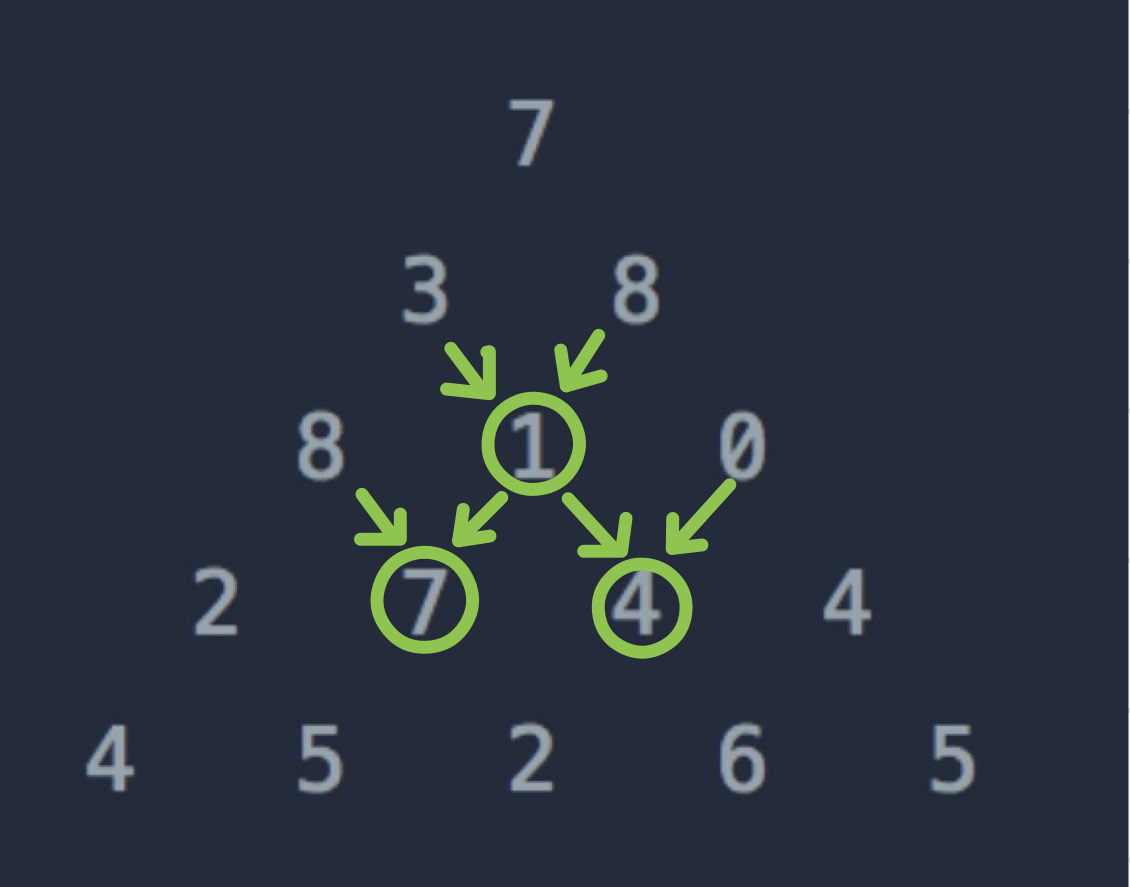
마지막은 위와 같이 최대 2개의 숫자를 선택하여 추가하는 경우입니다.
중간에 숫자가 있는 경우 왼쪽 상단과 오른쪽 상단의 숫자 중 하나를 선택하여 추가할 수 있습니다.
따라서 두 숫자 중 가장 큰 숫자를 선택하여 더할 수 있습니다.
재귀 수식의 형태로 표현:
// else
triangle(i)(j) += Math.max(triangle(i-1)(j-1), triangle(i-1)(j))
정답을 맞혀보세요
위의 과정을 통해 삼각형의 모든 위치에서 최대값을 찾았으니 이제 정답을 찾을 차례입니다.
답은 삼각형 밑면에 있는 숫자 중에서 최대값을 선택하는 것입니다.

따라서 루프를 통해 삼각형 int()()에 저장된 마지막 행의 숫자의 최대값을 반환합니다!
다음은 최종 Java 코드입니다!
(자바 코드)
class Solution {
public int solution(int()() triangle) {
int answer = 0;
int n = triangle.length;
for(int i=1;i<n;i++) {
for(int j=0;j<=i;j++) {
int temp = triangle(i)(j);
if(j==0) {
temp += triangle(i-1)(j);
}
else if(i==j) {
temp += triangle(i-1)(j-1);
} else {
temp += Math.max(triangle(i-1)(j-1), triangle(i-1)(j));
}
triangle(i)(j) = temp;
}
}
for(int i=1;i<n;i++) {
if(answer<triangle(n-1)(i)) {
answer = triangle(n-1)(i);
}
}
return answer;
}
}
실제로 이번에는 이전 솔루션과 코드가 동일합니다.
그러나 중요한 것은 무엇입니까? 다시 봐도 기억나는 자세한 해결 과정을 추가했습니다.
그럼 안녕!